Admission Tests Admission Tests Certifications GMAT Questions & Answers

• Question 321:

  For a certain cube, 3 deferent edges that do not at meet at a single vertex are to be painted red. How many different selections of the 3 different edges to be painted red are possible?

  A. 56

  B. 112

  C. 120

  D. 212

  E. 504

  Correct Answer: E

• Question 322:

  

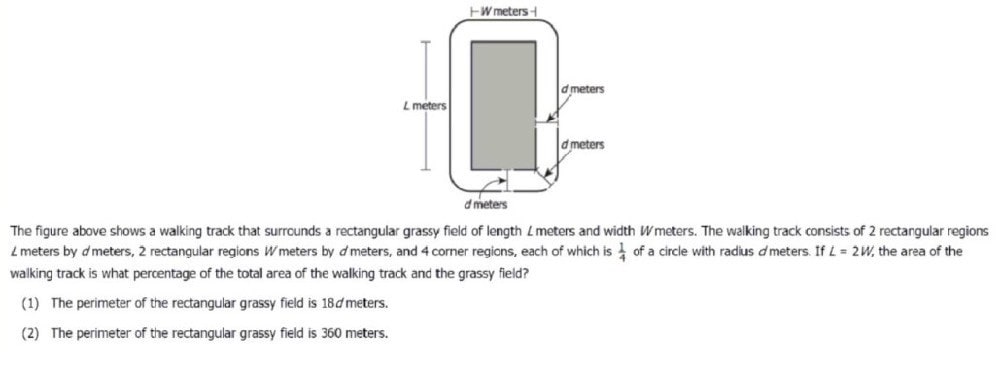
  A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.

  B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.

  C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

  D. EACH statement ALONE is sufficient.

  E. Statements (1) and (2) TOGETHER are NOT sufficient.

  Correct Answer: A

• Question 323:

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: D

• Question 324:

  A quantity of solution that is 3% salt by volume was mixed with a quantity of solution that is 9% salt by volume to produce a quantity of solution that is 4% salt by volume. How many liters of the 9% solution were used?

  (1)

  The quantity of 3% solution was 5 times the quantity of 9% solution.

  (2)

  The quantity of 4% solution produced was 150 liters.

  A.

  Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.

  B.

  Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.

  C.

  BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient

  D.

  EACH statement ALONE is sufficient.

  E.

  Statements (1) and (2) TOGETHER are NOT sufficient.

  Correct Answer: B

• Question 325:

  

  A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.

  B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.

  C. BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.

  D. EACH statement ALONE is sufficient

  E. Statements (1) and (2) TOGETHER are NOT sufficient.

  Correct Answer: C

• Question 326:

  

  The chart above shows political and geographic data on a certain legislative committee of 20 members, each of whom belongs to 1 of 2 political parties and lives in 1 of 4 regions. How many subcommittees of this legislative committee are possible that contain exactly 1 member from each of the 4 regions and the same number of members from each of the 2 political parties?

  A. 10

  B. 20

  C. 99

  D. 246

  E. 495

  Correct Answer: D

• Question 327:

  The sum of the first n positive integers is given by

  

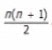
  What is the sum of the first 100 positive odd integers?

  A. 10,100

  B. 10,000

  C. 9,950

  D. 9,900

  E. 5,050

  Correct Answer: B

• Question 328:

  A lottery box contains 8,000 tickets, each of which is red or blue or green. The box contains twice as many blue tickets as red tickets. The number of green tickets is 20 more than the number of red and blue tickets combined. Which of the following Is the best approximation to the probability that the first ticket randomly drawn from the box will be blue?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: A

• Question 329:

  An intensive effort was made to expand the database of alumni names for a certain high school. The number of names in the database increased by 1,300 percent of the original number of 1,500 names. How many names were in the expanded database?

  A. 1,950

  B. 2,800

  C. 16,300

  D. 19,500

  E. 21,000

  Correct Answer: E

• Question 330:

  If 10 circles, all with different radii, are positioned in the same plane, what is the maximum possible number of distinct points where 2 or more of the circles intersect?

  A. 90

  B. 100

  C. 180

  D. 200

  E. 360

  Correct Answer: A