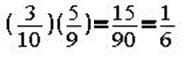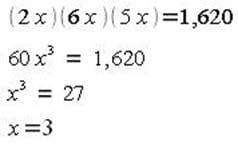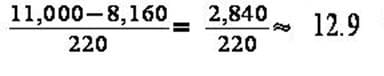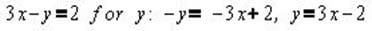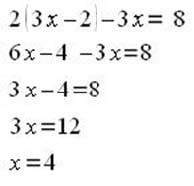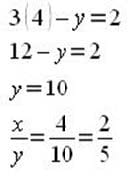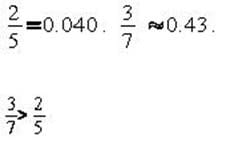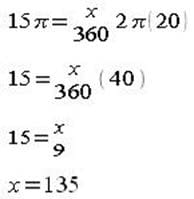Test Prep Test Prep Certifications SAT2-MATHEMATICS Questions & Answers

• Question 61:

  A box contains five blue pens, three black pens, and two red pens. If every time a pen is selected, it is removed from the box, what is the probability of selecting a black pen followed by a blue pen?

  

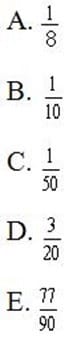
  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: A

  At the start, there are 5 + 3 + 2 = 10 pens in the box, 3 of which are black. Therefore, the probability of selecting a black pen is 3/10 After the black pen is removed, there are nine pens remaining in the box, five of which are blue. The

  

  probability of selecting a blue pen second is 5/9 To find the probability that both events will happen, multiply the probability of the first event by the probability of the second event:

• Question 62:

  The measures of the length, width, and height of a rectangular prism are in the ratio 2:6:5. If the volume of the prism is 1,620 mm3, what is the width of the prism?

  A. 3 mm

  B. 6 mm

  C. 9 mm

  D. 18 mm

  E. 27 mm

  Correct Answer: D

  The volume of a prism is equal to lwh, where is the length of the prism, w is the width of the prism, and h is the height of the prism:

  

  The length of the prism is2(3) = 6 mm, the width of the prism is6(3) = 18mm, and the height of the prism is5(3)=15mm.

• Question 63:

  An empty crate weighs 8.16 kg and an orange weighs 220 g. If Jon can lift 11,000 g, how many oranges can he pack in the crate before lifting it onto his truck?

  A. 12

  B. 13

  C. 37

  D. 46

  E. 50

  Correct Answer: A

  The empty crate weighs 8.16 kg, or 8,160 g. If Jon can lift 11,000 g and one orange weighs 220 g, then the number of oranges that he can pack into the crate is equal to

  

  Jon cannot pack a fraction of an orange. He can pack 12 whole oranges into the crate.

• Question 64:

  A. {-8, 1}

  B. {8, –1}

  C. {0, –8, 1}

  D. {0, 8, –1}

  E. {0, –1, –8, 1, 8}

  Correct Answer: C

• Question 65:

  What is the equation of the line that passes through the points (2, 3) and (?, 5)?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: B

  First, find the slope of the line. The slope of a line is equal to the change in y values divided by the change in x values of two points on the line. The y value increases by 2(5 - 3) and the x value decreases by 4(-2 2). Therefore, the slope of the line is equal to -2/4 or -1/2 The equation of the line is Y= -1/2x + b here b is they-intercept. Use either of the two given points to solve for b:

  

  The equation of the line that passes through the points (2, 3) and (-2, 5) is .

• Question 66:

  If 3x-y=2 and 2y-3x-8, which of the following is equal to x/y?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: B

  

  Solve

  Substitute 3x-2 for y in the second equation and solve for x:

  

  Substitute the value of x into the first equation to find the value of y:

  

  

• Question 67:

  All of the following are less than 2/5 EXCEPT:

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  E. Option E

  Correct Answer: D

  

  Comparing the hundredths digits,3>0 therefore, 0.43>0.40 and

• Question 68:

  SIMULATION

  

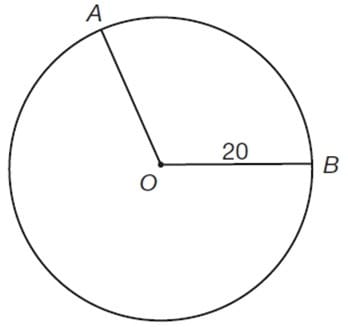
  In the diagram above, the radius of the circle is 20 units and the length of arc AB is 15 units. What is the measure in degrees of angle AOB?

  A. 135

  Correct Answer: A

  The length of an arc is equal to the circumference of the circle multiplied by the measure of the angle that intercepts the arc divided by 360. The arc measures 15 units, the circumference of a circle is 2 multiplied by the radius, and the radius of the circle is 20 units. If x represents the measure of angle AOB, then:

  

  The measure of angle AOB is 135 degrees.

• Question 69:

  SIMULATION

  Point A of rectangle ABCD is located at (–3, 12) and point C is located at (9,5).What is the area of rectangle ABCD?

  A. 84

  Correct Answer: A

  Explanation:

  If point A is located at (–3,12) and point C is located at (9,5), that means that either point B or point D has the coordinates (–3,5) and the other has the coordinates (9,12). The difference between the different x values is 9 – (–3) = 12 and the difference between the different y values is 12 – 5 = 7. The length of the rectangle is 12 units and the width of the rectangle is seven units. The area of a rectangle is equal to its length multiplied by its width, so the area of ABCD = (12)(7) = 84 square units.

• Question 70:

  SIMULATION

  DeDe and Mike both run the length of a two-mile field. If DeDe runs 5 mph and Mike runs 6 mph, how many more minutes does it take DeDe to run the field?

  A. 4

  Correct Answer: A

  DeDe runs 5 mph, or 5 miles in 60 minutes. Use a proportion to find how long it would take for DeDe to run

  minutes. Greg runs 6 mph, or 6 miles in 60minutes. Therefore, he runs 2 miles in

  

  2 miles:

  

  minutes. It takes DeDe 24 – 20 = 4 minutes longer to run the field.