Medical Tests Medical Tests Certifications MCAT-TEST Questions & Answers

• Question 251:

  One of the most common methods that scientists use to determine the age of fossils is known as carbon dating. 14C is an unstable isotope of carbon that undergoes beta decay with a half-life of approximately 5,730 years. Beta decay occurs when a neutron in the nucleus decays to form a proton and an electron which is ejected from the nucleus. 14C is generated in the upper atmosphere when 14N, the most common isotope of nitrogen, is bombarded by neutrons. This mechanism yields a global production rate of 7.5 kg per year of 14C, which combines with oxygen in the atmosphere to produce carbon dioxide. Both the production and the decay of 14C occur simultaneously. This process continues for many half-lives of 14C, until the total amount of 14C approaches a constant. A fixed fraction of the carbon ingested by all living organisms will be 14C. Therefore, as long as an organism is alive, the ratio of 14C to 12C that it contains is constant. After the organism dies, no new 14C is ingested, and the amount of 14C contained in the organism will decrease by beta decay. The amount of 14C that must have been present in the organism when it died can be calculated from the amount of 12C present in a fossil. By comparing the amount of 14C in the fossil to the calculated amount of

  14C that was present in the organism when it died, the age of the fossil can be determined.

  In determining the age of the galaxy, a technique similar to carbon dating is used on stars with the radioactive isotope 232Th, which has a half-life of 1010 years. 14C is less suitable for this application because:

  A. its half-life is too long.

  B. 14C is more abundant than 232Th is in stars.

  C. 14C is unstable.

  D. its half-life is too short.

  Correct Answer: D

  The age of the galaxy is much greater than that of fossils on the Earth. Therefore, in determining the age of the galaxy, it makes sense to use an isotope with a longer half-life than 14C, which is used in determining the age of Earth fossils.

  This is because 14C will decay to undetectable quantities more quickly than an isotope with a longer half-life, like 232Th. Hence, choice D is correct, and choice A is incorrect.

  Choice B is wrong because there is no reason to think that 14C is more abundant in stars.

  And if it were true, 14C would be more suitable for this application because the larger abundance would be easier to measure. Choice C is wrong because the instability of 14C, and 232Th for that matter, is precisely what makes them useful

  as dating tools.

• Question 252:

  One of the most common methods that scientists use to determine the age of fossils is known as carbon dating. 14C is an unstable isotope of carbon that undergoes beta decay with a half-life of approximately 5,730 years. Beta decay occurs when a neutron in the nucleus decays to form a proton and an electron which is ejected from the nucleus. 14C is generated in the upper atmosphere when 14N, the most common isotope of nitrogen, is bombarded by neutrons. This mechanism yields a global production rate of 7.5 kg per year of 14C, which combines with oxygen in the atmosphere to produce carbon dioxide. Both the production and the decay of 14C occur simultaneously. This process continues for many half-lives of 14C, until the total amount of 14C approaches a constant. A fixed fraction of the carbon ingested by all living organisms will be 14C. Therefore, as long as an organism is alive, the ratio of 14C to 12C that it contains is constant. After the organism dies, no new 14C is ingested, and the amount of 14C contained in the organism will decrease by beta decay. The amount of 14C that must have been present in the organism when it died can be calculated from the amount of 12C present in a fossil. By comparing the amount of 14C in the fossil to the calculated amount of 14C that was present in the organism when it died, the age of the fossil can be determined. The method of carbon dating used to determine age depends upon the assumption that:

  A. the half-life of 14C changes when it is ingested.

  B. all ingested 14C is incorporated into the body.

  C. the half-life of 14C depends on the type of molecule in which it resides.

  D. the half-life of 14C does not depend upon conditions external to the 14C nucleus.

  Correct Answer: D

  Carbon dating uses the fact that 14C is unstable and decays over time, while 12C is stable and does not decay. Let's say the ratio of 14C to 12C in an organism is known at the moment of death. By measuring the ratio of 14C to 12C in a fossil, the age of the fossil can be determined because the 14C in the dead organism decays over time in a quantifiable way. Although it is not explicitly stated in the passage, choice D is an assumption of carbon dating. It correctly states that the half-life of 14C does not depend upon conditions external to the 14C nucleus. This means that the half-life does not depend on the weather, the amount of 14C present, etc. Because the half-life is a constant with respect to conditions external to the nucleus, it can be used to measure elapsed time accurately. Since measuring time is the goal of carbon dating, choice D is a necessary assumption. Choice A is wrong because ingestion is an event that is external to the nucleus. Choice C is wrong because the type of molecule in which 14C is incorporated is also a condition external to the nucleus. Choice B is wrong because we know from biology that some carbon leaves the body as waste. This does not affect carbon dating, however, because what matters is the ratio of 14C to 12C left in the body, not the specific amount of 14C left in the body.

• Question 253:

  One of the most common methods that scientists use to determine the age of fossils is known as carbon dating. 14C is an unstable isotope of carbon that undergoes beta decay with a half-life of approximately 5,730 years. Beta decay occurs when a neutron in the nucleus decays to form a proton and an electron which is ejected from the nucleus. 14C is generated in the upper atmosphere when 14N, the most common isotope of nitrogen, is bombarded by neutrons. This mechanism yields a global production rate of 7.5 kg per year of 14C, which combines with oxygen in the atmosphere to produce carbon dioxide. Both the production and the decay of 14C occur simultaneously. This process continues for many half-lives of 14C, until the total amount of 14C approaches a constant. A fixed fraction of the carbon ingested by all living organisms will be 14C. Therefore, as long as an organism is alive, the ratio of 14C to 12C that it contains is constant. After the organism dies, no new 14C is ingested, and the amount of 14C contained in the organism will decrease by beta decay. The amount of 14C that must have been present in the organism when it died can be calculated from the amount of 12C present in a fossil. By comparing the amount of 14C in the fossil to the calculated amount of 14C that was present in the organism when it died, the age of the fossil can be determined. The bones of a living human adult contain about 8 grams of 14C at any given time. If a prehistoric human adult skeleton is found to contain 1 gram of 14C, what is the approximate age of the fossil?

  A. 5,730 years

  B. 17,190 years

  C. 34,380 years

  D. 45,840 years

  Correct Answer: A

  The passage states that after death, the 14C in a skeleton that beta decays is not replaced by new 14C. Consequently, as time passes, the amount of 14C in the skeleton decreases. The half-life quantifies the rate of this decrease. The half-life of an isotope is the length of time it takes for half of the atoms in a sample of that isotope to decay. A skeleton starts out with 8 g of 14C, and the half-life of 14C is 5,730 years. Therefore, after 5,730 years, 8 g of 14C will decay to 4 g. After another 5,730 years, 4 g will decay to 2 g, and after yet another 5,730 years, 2 g will decay to 1 g, which is the amount present in the prehistoric skeleton. Hence, the prehistoric skeleton must be 3(5,730) = 17,190 years old, and choice B is correct.

• Question 254:

  One of the most common methods that scientists use to determine the age of fossils is known as carbon dating. 14C is an unstable isotope of carbon that undergoes beta decay with a half-life of approximately 5,730 years. Beta decay occurs when a neutron in the nucleus decays to form a proton and an electron which is ejected from the nucleus. 14C is generated in the upper atmosphere when 14N, the most common isotope of nitrogen, is bombarded by neutrons. This mechanism yields a global production rate of 7.5 kg per year of 14C, which combines with oxygen in the atmosphere to produce carbon dioxide. Both the production and the decay of 14C occur simultaneously. This process continues for many half-lives of 14C, until the total amount of 14C approaches a constant. A fixed fraction of the carbon ingested by all living organisms will be 14C. Therefore, as long as an organism is alive, the ratio of 14C to 12C that it contains is constant. After the organism dies, no new 14C is ingested, and the amount of 14C contained in the organism will decrease by beta decay. The amount of 14C that must have been present in the organism when it died can be calculated from the amount of 12C present in a fossil. By comparing the amount of 14C in the fossil to the calculated amount of 14C that was present in the organism when it died, the age of the fossil can be determined.

  If the global production rate of 14C were to increase to 10 kg per year:

  A. the number of 14C atoms decaying per minute would increase.

  B. the number of 14C atoms decaying per minute would decrease.

  C. the weight of 14C on the Earth would increase indefinitely.

  D. the amount of 14C ingested by living organisms would not change.

  Correct Answer: A

  The number of atoms decaying per unit time is directly proportional to the number of atoms present. To see this, recall that the definition of half-life is the time required for half of a sample to decay. The half-life is a constant for a given material

  regardless of the sample size. Therefore, if the initial amount of material is greater, then a larger amount of material will decay during each half-life. If the production rate of 14C increases, then there will be more 14C present. Hence, the

  number of 14C atoms decaying per unit time will increase. So choice A is correct and choice B is incorrect.

  The second paragraph describes how a balance between 14C production and decay is reached, so that the total amount of 14C on Earth approaches a constant. If 14C production is increased, then the weight of 14C on Earth will initially

  increase. However, as this 14C begins to decay, the total amount of 14C will approach a new constant as a new balance is reached between the production and decay processes. Hence, choice C is wrong. If the production of 14C increases,

  then a larger fraction of the carbon on Earth will be 14C, and living organisms will ingest a larger fraction of 14C. Therefore, the percentage of 14C in living organisms will increase, and choice D is wrong.

• Question 255:

  A helium-neon gas discharge laser as shown in Figure 1 below generates a coherent beam of monochromatic light at a wavelength of 632.8 nm.

  

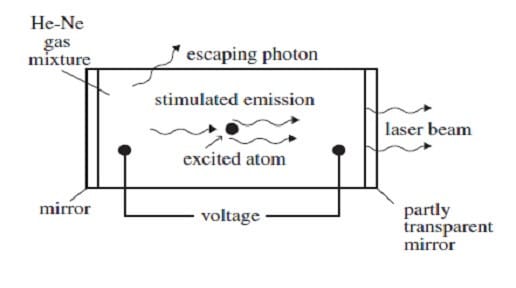
  Figure 1

  A discharge current of electrons is created in the tube by an applied voltage. When these electrons collide with the helium atoms, they can excite ground-state helium electrons to an energy level of 20.61 eV. The excited electrons cannot decay back to the ground state by emitting a photon because such a transition does not conserve angular momentum. Instead, if the excited helium atom collides with a neon atom, a ground-state electron in the neon atom can be excited to an energy level of 20.66 eV, and the helium electron can return to its ground state. The above process occurs quite often in the tube until the percentage of neon atoms with electrons in the 20.66-eV energy level is greater than the percentage of neon atoms with electrons in lower levels. This condition is called a population inversion. An excited electron in one of the neon atoms can then spontaneously decay by emitting a photon of wavelength 632.8 nm in a random direction. The photon will stimulate the same transition in another excited electron in a neon atom. The photon radiated by this stimulated emission process travels in the same direction as the original photon. The resulting light is then reflected back and forth inside the tube until it escapes through the partially transparent mirror. (Note: A photon's energy in eV is given by E = 1240/, where is the photon's wavelength in nm. The helium and neon ground-state energies are both 0 eV.)

  Why is stimulated emission of photons necessary in order to produce a coherent beam of light instead of spontaneous emission alone?

  A. Stimulated emission produces photons of higher energy than those produced by spontaneous emission.

  B. Stimulated emission produces photons that travel in the same direction as the photon that induces their emission.

  C. Stimulated emission produces photons with longer wavelengths than those produced by spontaneous emission.

  D. Either spontaneous or stimulated emission alone would be sufficient to produce laser light.

  Correct Answer: B

  To answer this question, you have to figure out the difference between stimulated and spontaneous emission. The passage states that a photon is emitted in a random direction when an atom spontaneously decays. This process is called spontaneous emission. It also states that a photon can stimulate an electron transition in an atom. The photon that is emitted in this process, called stimulated emission, travels in the same direction as the stimulating photon. Therefore, spontaneous emission produces photons that travel in random directions, whereas stimulated emission produces photons that travel in the same direction as the stimulating photon. A coherent beam of light consists of photons travelling in the same direction. So choice B is correct. Choices A and C are wrong because, as stated in the third paragraph, the photon produced by spontaneous emission causes stimulated emission by inducing the same electron transition in another excited atom. Since the electron transition is the same, the photon energy released by the transition is the same, and the photon wavelengths must be the same because energy and wavelength are related by the formula E = 1240/. Choice D is incorrect because stimulated emission is necessary to obtain a large number of photons traveling in the same direction.

• Question 256:

  A helium-neon gas discharge laser as shown in Figure 1 below generates a coherent beam of monochromatic light at a wavelength of 632.8 nm.

  

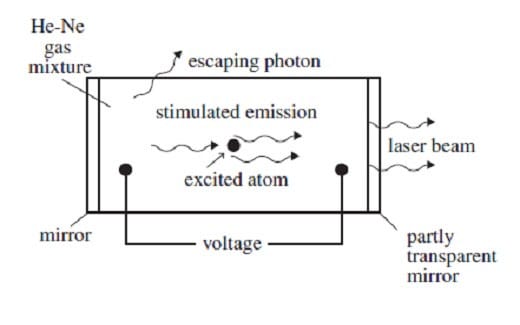
  Figure 1

  A discharge current of electrons is created in the tube by an applied voltage. When these electrons collide with the helium atoms, they can excite ground-state helium electrons to an energy level of 20.61 eV. The excited electrons cannot decay back to the ground state by emitting a photon because such a transition does not conserve angular momentum. Instead, if the excited helium atom collides with a neon atom, a ground-state electron in the neon atom can be excited to an energy level of 20.66 eV, and the helium electron can return to its ground state. The above process occurs quite often in the tube until the percentage of neon atoms with electrons in the 20.66-eV energy level is greater than the percentage of neon atoms with electrons in lower levels. This condition is called a population inversion. An excited electron in one of the neon atoms can then spontaneously decay by emitting a photon of wavelength 632.8 nm in a random direction. The photon will stimulate the same transition in another excited electron in a neon atom. The photon radiated by this stimulated emission process travels in the same direction as the original photon. The resulting light is then reflected back and forth inside the tube until it escapes through the partially transparent mirror. (Note: A photon's energy in eV is given by E = 1240/, where is the photon's wavelength in nm. The helium and neon ground-state energies are both 0 eV.)

  A laser produces light with a wavelength of 200 nm at a power of 6.2 x 1015 eV/s. How many photons per second does this laser deliver?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: A

  The power of the laser is 6.2 X 1015 eV/s, which means that the laser produces 6.2 X 1015 eV of energy each second. This energy takes the form of photon energy. To solve for the number of photons produced per second, figure out how many photons correspond to an energy of 6.2 X 1015 eV. The formula given in the passage states that the energy (in eV) of one photon is given by E = 1240/, where is the photon's wavelength in nm. Hence, the energy of n photons must given by n (1240/). Setting this expression equal to 6.2 X 1015 eV and solving for n, we obtain n = (6.2 X 1015 /1240). The question stem states that for this laser, = 200 nm. Substituting in, we calculate n = 200(6.2 X 1015 /1240) = 1.0 X 1015 , which is choice A.

• Question 257:

  A helium-neon gas discharge laser as shown in Figure 1 below generates a coherent beam of monochromatic light at a wavelength of 632.8 nm.

  

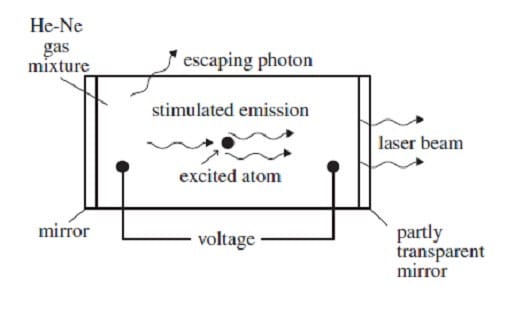
  Figure 1

  A discharge current of electrons is created in the tube by an applied voltage. When these electrons collide with the helium atoms, they can excite ground-state helium electrons to an energy level of 20.61 eV. The excited electrons cannot decay back to the ground state by emitting a photon because such a transition does not conserve angular momentum. Instead, if the excited helium atom collides with a neon atom, a ground-state electron in the neon atom can be excited to an energy level of 20.66 eV, and the helium electron can return to its ground state. The above process occurs quite often in the tube until the percentage of neon atoms with electrons in the 20.66-eV energy level is greater than the percentage of neon atoms with electrons in lower levels. This condition is called a population inversion. An excited electron in one of the neon atoms can then spontaneously decay by emitting a photon of wavelength 632.8 nm in a random direction. The photon will stimulate the same transition in another excited electron in a neon atom. The photon radiated by this stimulated emission process travels in the same direction as the original photon. The resulting light is then reflected back and forth inside the tube until it escapes through the partially transparent mirror. (Note: A photon's energy in eV is given by E = 1240/, where is the photon's wavelength in nm. The helium and neon ground-state energies are both 0 eV.)

  A helium atom with an electron in the 20.61-eV energy level collides with a neon atom with an electron in the ground state. The result is that the helium electron returns to the ground state, and the groundstate neon electron is excited to an energy level of 20.66 eV. What is the minimum kinetic energy lost by the helium atom?

  A. 0.05 eV

  B. 1.96 eV

  C. 10.3 eV

  D. 20.61 eV

  Correct Answer: A

  To solve this problem, apply the law of conservation of energy to atomic systems. In the absence of dissipative forces, the total energy of a system, which is the sum of the kinetic and potential energies, is conserved. In the case of atoms, the potential energy is the energy stored when the electron moves to a higher energy state by absorbing a photon. In the collision between the helium and neon atoms, the helium atom loses 20.61 eV of potential energy because its electron returns to the ground state and the neon atom gains 20.66 eV of potential energy. Since energy is conserved, the helium atom must have lost some kinetic energy as well. The neon atom cannot gain more energy than the helium atom loses. Therefore, the minimum amount of kinetic energy that the helium atom must lose is equal to the difference between the two potential energies. This is equal to 20.66 ?20.61 = 0.05 eV, which is choice A. If the helium atom loses only this amount of kinetic energy, then the neon atom's kinetic energy will not change during the collision. If the helium atom loses more than 0.05 eV, then the neon atom's kinetic energy will increase.

• Question 258:

  A helium-neon gas discharge laser as shown in Figure 1 below generates a coherent beam of monochromatic light at a wavelength of 632.8 nm.

  

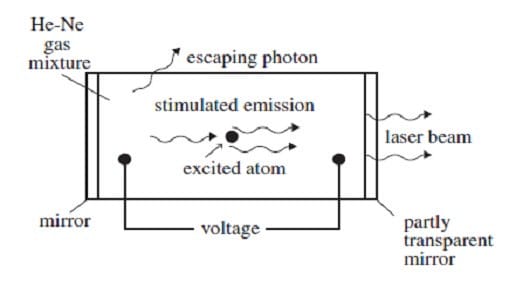
  Figure 1

  A discharge current of electrons is created in the tube by an applied voltage. When these electrons collide with the helium atoms, they can excite ground-state helium electrons to an energy level of 20.61 eV. The excited electrons cannot decay back to the ground state by emitting a photon because such a transition does not conserve angular momentum. Instead, if the excited helium atom collides with a neon atom, a ground-state electron in the neon atom can be excited to an energy level of 20.66 eV, and the helium electron can return to its ground state. The above process occurs quite often in the tube until the percentage of neon atoms with electrons in the 20.66-eV energy level is greater than the percentage of neon atoms with electrons in lower levels. This condition is called a population inversion. An excited electron in one of the neon atoms can then spontaneously decay by emitting a photon of wavelength 632.8 nm in a random direction. The photon will stimulate the same transition in another excited electron in a neon atom. The photon radiated by this stimulated emission process travels in the same direction as the original photon. The resulting light is then reflected back and forth inside the tube until it escapes through the partially transparent mirror. (Note: A photon's energy in eV is given by E = 1240/, where is the photon's wavelength in nm. The helium and neon ground-state energies are both 0 eV.)

  What is the energy of the photon with wavelength 632.8 nm?

  A. 0.05 eV

  B. 1.96 eV

  C. 20.61 eV

  D. 20.66 eV

  Correct Answer: B

  This question is a straightforward application of the equation given in the passage, E =1240/. In this equation, E is the energy in electron-volts of a photon having a wavelength in nanometers. Note that this formula is a variant of the more familiar equation E = hc/ . Plugging = 632.8 nm, we obtain E = 1240/632.8 2.0 eV, which is closest to choice B. It is a good idea to save time by estimating because the answer choices are relatively far apart.

• Question 259:

  A helium-neon gas discharge laser as shown in Figure 1 below generates a coherent beam of monochromatic light at a wavelength of 632.8 nm.

  

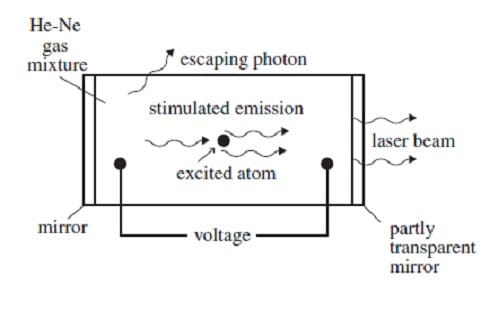
  Figure 1

  A discharge current of electrons is created in the tube by an applied voltage. When these electrons collide with the helium atoms, they can excite ground-state helium electrons to an energy level of 20.61 eV. The excited electrons cannot decay back to the ground state by emitting a photon because such a transition does not conserve angular momentum. Instead, if the excited helium atom collides with a neon atom, a ground-state electron in the neon atom can be excited to an energy level of 20.66 eV, and the helium electron can return to its ground state. The above process occurs quite often in the tube until the percentage of neon atoms with electrons in the 20.66-eV energy level is greater than the percentage of neon atoms with electrons in lower levels. This condition is called a population inversion. An excited electron in one of the neon atoms can then spontaneously decay by emitting a photon of wavelength 632.8 nm in a random direction. The photon will stimulate the same transition in another excited electron in a neon atom. The photon radiated by this stimulated emission process travels in the same direction as the original photon. The resulting light is then reflected back and forth inside the tube until it escapes through the partially transparent mirror. (Note: A photon's energy in eV is given by E = 1240/, where is the photon's wavelength in nm. The helium and neon ground-state energies are both 0 eV.)

  A population inversion exists in the laser tube when:

  A. the percentage of neon atoms with electrons in the ground state is greater than the percentage of neon atoms with electrons in higher energy levels.

  B. the percentage of neon atoms with electrons in a higher energy level is greater than the percentage of neon atoms with electrons in lower energy levels.

  C. the percentage of neon atoms with electrons in a higher energy level is equal to the percentage of neon atoms with electrons in the ground state.

  D. all the neon atoms have electrons in the ground state only.

  Correct Answer: B

  To answer this question, you have to refer back to the passage to find the description of the condition called a population inversion. The passage states that a population inversion exists when the percentage of neon atoms with electrons in the 20.66 eV energy level is greater than the percentage of neon atoms with electrons in lower levels. The distinctive characteristic of this distribution is that the percentage of atoms with electrons in a higher energy level is greater than the percentage of atoms with electrons in lower levels. The only choice that is consistent with this is choice B, so it is the correct answer.

• Question 260:

  Band theory explains the conductivity of certain solids by stating that the atomic orbitals of the individual atoms in the solid merge to produce a series of atomic orbitals comprising the entire solid. The closely-spaced energy levels of the orbitals form bands. The band corresponding to the outermost occupied subshell of the original atoms is called the valence band. If partially full, as in metals, it serves as a conduction band through which electrons can move freely. If the valence band is full, then electrons must be raised to a higher band for conduction to occur. The greater the band gap between the separate valence and conduction bands, the poorer the material's conductivity. Figure 1 shows the valence and conduction bands of a semiconductor, which is intermediate in conductivity between conductors and insulators.

  

  Figure 1

  When silicon, a semiconductor with tetrahedral covalent bonds, is heated, a few electrons escape into the conduction band. Doping the silicon with a few phosphorus atoms provides unbonded electrons that escape more easily, increasing conductivity. Doping with boron produces holes in the bonding structure, which may be filled by movement of nearby electrons within the lattice. When a semiconductor in an electric circuit has excess electrons on one side and holes on the other, electron flow occurs more easily from the side with excess electrons to the side with holes than in the reverse direction.

  

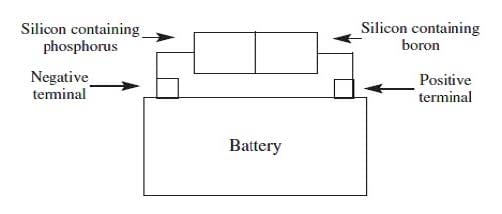
  Figure 2 If the semiconductor orientation in Figure 2 were reversed so that the boron-doped silicon was on the left and the phosphorus-doped silicon on the right, what could be said about the electron flow of the new setup?

  A. The electron flow is easier in the new direction than in that of Figure 2.

  B. The electron flow is the same in either direction.

  C. The electron flow is more difficult in the new direction than in that of Figure 2.

  D. The electrons cannot flow in the new setup.

  Correct Answer: C

  The passage provides almost all the necessary information to answer this question. The only piece of background information needed is that electrons flow from the negative terminal to the positive terminal. The passage states that phosphorus-doped silicon has more electrons than pure silicon and that boron-doped silicon has fewer electrons than pure silicon. In addition, it is stated that electrons flow more easily from a side with excess electrons -- the phosphorus-doped silicon -- to a side with fewer electrons -- the boron-doped silicon. So, if the semiconductor orientation were switched, electron flow would not be as easy as the original configuration. Choice C is therefore the correct response.