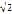Medical Tests Medical Tests Certifications MCAT-TEST Questions & Answers

• Question 321:

  Several techniques have been developed to determine the order of a reaction. The rate of a reaction cannot be predicted on the basis of the overall equation, but can be predicted on the basis of the rate-determining step. For instance, the following reaction can be broken down into three steps.

  

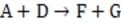
  Step 1

  

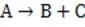
  (Slow) Step 2

  

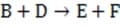
  (fast) Step 3

  

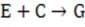
  (fast)

  Reaction 1 In this case, the first step in the reaction pathway is the rate-determining step. Therefore, the overall rate of the reaction must equal the rate of the first step, k1 [A] where k1 is the rate constant for the first step. (Rate constants of the different steps are denoted by kx , where x is the step number.)

  In some cases, it is desirable to measure the rate of a reaction in relation to only one species. In a second-order reaction, for instance, a large excess of one species is included in the reaction vessel. Since a relatively small amount of this large concentration is reacted, we assume that the concentration essentially remains unchanged. Such a reaction is called a pseudo first-order reaction. A new rate constant, k', is established, equal to the product of the rate constant of the original reaction, k, and the concentration of the species in excess. This approach is often used to analyze enzyme activity.

  In some cases, the reaction rate may be dependent on the concentration of a short-lived intermediate. This can happen if the rate-determining step is not the first step. In this case, the concentration of the intermediate must be derived from the equilibrium constant of the preceding step. For redox reactions, the equilibrium can be correlated with the voltage produced by two half-cells by means of the Nernst equation. This equation states that at any given moment:

  

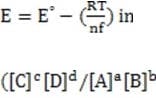
  Equation 1 When

  

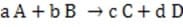
  Reaction 2

  Note: R = 8.314 J/K•mol; F = 9.6485 x 104 C/mol.)

  In a test of the rate of Step 3 of Reaction 1, a solution is prepared containing a 0.1 M concentration of E and a 50 M concentration of C. The rate is calculated after the reaction has gone 50% to completion. By what percent will the calculated

  rate differ from the true rate if we treat the reaction as pseudo first-order?

  A. 0.02%

  B. 0.05%

  C. 0.1%

  D. 0.2%

  Correct Answer: C

  This question may seem confusing, but you can find the right answer if you proceed carefully. We know that there is such an excess of reactant C that its concentration is virtually constant. So, as the passage says, we can treat this as a pseudo first-order reaction with respect to E. However, the rate predicted this way will be slightly larger than the true rate because the true concentration of C has been reduced slightly. In the question, we start with a concentration of E equal to 0.1 mol/L and a concentration of C equal to 50 mol/L. When the reaction has gone 50% toward completion, the concentration of E will be 0.05 mol/L and the concentration of C will be 49.95 mol/L. So the actual rate of the reaction will be k x

  0.05 x 49.95, not k x 50 as the pseudo first-order would predict. The percent difference between these two rates is just the amount of the difference divided by the true rate. So we find the difference between the two rates by subtracting the actual rate, (k x 0.05 x 49.95), from the calculated rate, (k x 0.05 x 50). This gives us a difference of k x 0.05 x 0.05. Next, divide this amount by the actual rate, k x 0.05 x 49.95. We can cancel out the first two factors, and we are left with 0.05 divided by 49.95, or approximately 0.001. Now multiply this by 100% to convert to a percent, and we're left with 0.1 %, choice C.

• Question 322:

  A gibbon (lesser ape) of mass m and arm length l reaches to a branch level with its shoulder and starts to swing with its arm fully extended. At the bottom of the swing, its velocity is: A. Option A

  

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: A

  This question is a simple energy analysis. The height of the gibbon will decrease by the length of its arm as it reaches the bottom of the swing. Its potential energy of mgl will be converted to kinetic energy. mgl = 1/2mv2

  

  Choice B is the kinetic energy at the bottom of the swing. Choice C is just wrong. Choice D calculates for the period of an ideal pendulum.

• Question 323:

  Several techniques have been developed to determine the order of a reaction. The rate of a reaction cannot be predicted on the basis of the overall equation, but can be predicted on the basis of the rate-determining step. For instance, the following reaction can be broken down into three steps.

  

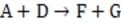
  Step 1

  

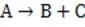
  (Slow) Step 2

  

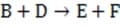
  (fast) Step 3

  

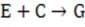
  (fast)

  Reaction 1 In this case, the first step in the reaction pathway is the rate-determining step. Therefore, the overall rate of the reaction must equal the rate of the first step, k1 [A] where k1 is the rate constant for the first step. (Rate constants of the different steps are denoted by kx , where x is the step number.)

  In some cases, it is desirable to measure the rate of a reaction in relation to only one species. In a second-order reaction, for instance, a large excess of one species is included in the reaction vessel. Since a relatively small amount of this large concentration is reacted, we assume that the concentration essentially remains unchanged. Such a reaction is called a pseudo first-order reaction. A new rate constant, k', is established, equal to the product of the rate constant of the original reaction, k, and the concentration of the species in excess. This approach is often used to analyze enzyme activity.

  In some cases, the reaction rate may be dependent on the concentration of a short-lived intermediate. This can happen if the rate-determining step is not the first step. In this case, the concentration of the intermediate must be derived from the equilibrium constant of the preceding step. For redox reactions, the equilibrium can be correlated with the voltage produced by two half-cells by means of the Nernst equation. This equation states that at any given moment:

  

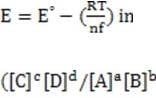
  Equation 1 When

  

  Reaction 2

  Note: R = 8.314 J/K?mol; F = 9.6485 x 104 C/mol.)

  An enzyme, R, catalyzes the oxidation of A to B. Reacting various concentrations of A and B with a large excess of R produced the following results during the first few minutes of the reaction.

  

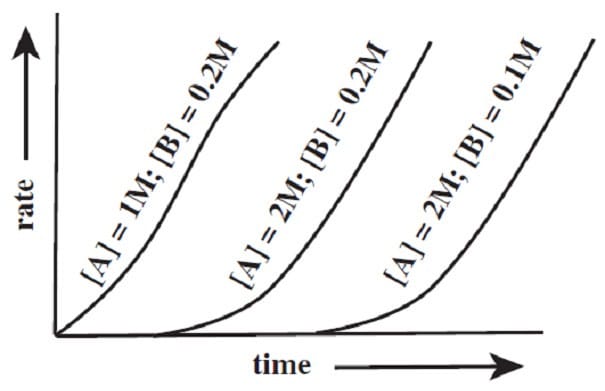
  Which of the following is the best tentative rate equation?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: C

  The enzyme participates in the reaction, but its concentration is so high that it can be treated as a constant and not included in the rate equation, so right away, choice D can be eliminated. To choose from the other three choices, we need to look at the graph and see whether the rate of the reaction is proportional to the concentration of A, or the concentration of B, or both. When we look at the graph, the results appear strange. A reaction usually slows down as time goes by, but this reaction starts slowly, and then speeds up. The length of the lag period increases as A increases and B decreases. This is just the opposite of what we would expect: most reaction rates slow down as the product accumulates. What does this mean? Remember that we don't see the ultimate rate of the reaction; we see a temporary lag period. The length of this lag period seems to be proportional to the ratio of A to B. The higher the concentration of product, the faster the reaction rate. This suggests that the product is somehow participating in the reaction. The more B that is present, the faster A can react. Once the reaction gets started, more B is present and the rate then speeds up. At equal concentrations of B, the sample with a higher concentration of A takes longer to get started because a lower ratio of B is available. We don't know exactly how A and B interact; but we know that changing the concentration of either A or B affects the lag period and the rate, so both must factor into the rate equation. Thus, the best answer is choice C. The reason X and Y are used as exponents is that we do not know the actual effect the two species have on the rate, only that they do affect it, so the exponents are left unknown. That is also why this is a tentative rate equation, not an actual rate equation.

• Question 324:

  Which titration curve would be produced by titrating 25 mL of a 0.1 N weak base with a 0.1 N strong acid?

  

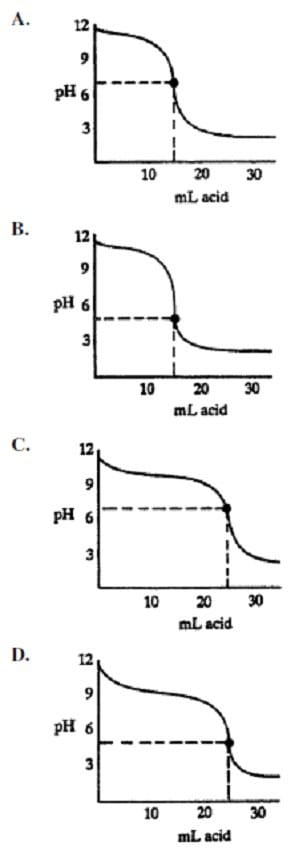
  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: D

  In this question you are asked about the titration of a weak base with a strong acid. The points marked by the dotted lines in each graph are the equivalence points. These are the points at which the acid has been totally neutralized by the added base. To decide which of these graphs is accurate, there are two things you need to know. First, you need to decide how much of a weak base is required to neutralize a strong acid. Second, you must know what the pH will be after the acid has been completely neutralized. First, let's consider the amount of strong acid needed to neutralize a weak base. The question tells you that both the weak base and the strong acid are 0.1 N. Since the weak base is only partially dissociated, the actual hydroxide ion concentration of the base will be considerably lower than the hydrogen ion concentration of the strong acid. For this reason, it may seem likely that the volume of acid that you would have to add to the base to bring about neutralization would be lower than the volume of the base you started with. In choices A and B, only 15 mL of acid are added to bring 25 mL of base to the equivalence point. However, the problem with this line of reasoning is that as soon as the small amount of free hydroxide in the basic solution has been neutralized, more of the base will dissociate and there will be more hydroxide. As you continue to add acid, eventually all of the base will dissociate. Thus, you'll end up having to add enough acid to neutralize all of the hydroxide in the base, just as if it were a strong base. Since the number of equivalents are equal in this case due to the equal normalities, the neutralization of 25 mL of weak base will require a full 25 mL of strong acid and that means that you can eliminate choices A and B. Next, you'll have to decide what the pH of the neutralized solution will be. When the base has been completely neutralized, a solution of salt water remains. But the cation, since it comes from a weak base, has a strong tendency to recombine with hydroxide ions from the water. The anion, since it comes from a strong acid, remains completely dissociated. This means that the process of hydrolysis takes place; the cation combines with the hydroxide from water molecules while the resulting hydrogen ions remain free in solution. Thus, a neutralized solution formed from a weak base and a strong acid will be slightly acidic and choice D is correct.

• Question 325:

  Suppose an -particle starting from rest is accelerated through a 5 megavolt potential difference. What is the final kinetic energy of the -particle? (Note: Assume that e = 1.6x10-19 C.)

  A. 1.6 x 10-12 J

  B. 8.0 x 10-13 J

  C. 6.4 x 10-26 J

  D. 3.2 x 10-26 J

  Correct Answer: A

  This question is a straightforward application of the conservation of energy. The absolute value of the change in kinetic energy equals the absolute value of the change in potential energy. Since the particle starts from rest, the change in kinetic energy is just the final kinetic energy. An -particle is a helium-4 nucleus consisting of 2 protons and 2 neutrons. The change in potential energy is equal to the charge times the potential difference. The charge of an -particle is equal to the charge times the potential difference. The charge of an -particle is equal to two times the charge of a proton, or 2e. So the final kinetic energy is therefore equal to the potential difference of 5 x 106 volts times the alpha particle charge of 2 x 1.6 x 10-19 coulombs. This is 1.6 x 10-12 joules, choice A.

• Question 326:

  Based on the table below, what is the cell voltage for the following reaction?

  

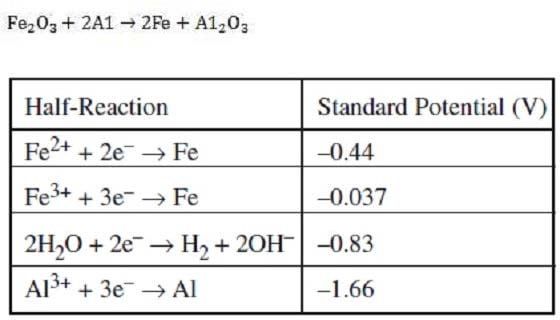
  A. –1.33 V

  B. 1.99 V

  C. 1.33 V

  D. 1.62 V

  Correct Answer: D

• Question 327:

  A particle of mass m moves in a circle of radius r at a uniform speed and makes 1 revolution per second. What is the energy of the particle?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: B

  We need to calculate the kinetic energy of the particle, so we'll need to use the equation K=1/2mv2, where K is the kinetic energy, m is the mass, and v is the velocity. In the question we are told that the mass is m, but we're given nothing for the speed. We can figure it out though: Since the speed of the particle is uniform, it is related to the distance d, and the time t by the equation v = d/t. Now the distance that the particle moves through in one revolution is 2r, where r is the radius of the circular path, and since the particle goes through one revolution per second, its velocity equals 2r. Now we can substitute this expression for velocity into our equation for kinetic energy, and get that K=1/2m(2r)2. This gives us the equation that K=22mr2, choice B.

• Question 328:

  Aski jump is an inclined track from which a ski jumper takes off through the air. After traveling down the track, the skier takes off from a ramp at the bottom of the track. The skier lands farther down on the slope.

  Figure 1 shows a ski jump, in which the ramp at the lower end of the track makes an angle of 30° to the horizontal. The track is inclined at an angle of to the horizontal and the slope is inclined at an angle of 45° to the horizontal. A ski jumper is stationary at the top of the track. Once the skier pushes off, she accelerates down the track, and then takes off from the ramp. The vertical height difference between the top of the track and its lowest point is 50 m, and the vertical height difference between the top of the ramp and its lowest point is 10 m.

  

  Figure 1

  The distance traveled by the skier between leaving the ski jump ramp and making contact with the slope is called the jump distance. In some cases, in order to increase the jump distance a skier will jump slightly upon leaving the ramp,

  thereby increasing the vertical velocity. Unless otherwise stated, assume that friction between the skis and the slope is negligible, and ignore the effects of air resistance.

  What is the acceleration of an 80-kg skier going down the track if = 45?

  

  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: A

  The track is just an incline, so this is an incline-plane problem. Neglecting friction and air resistance, the only force parallel to the track is the component of the skier's weight parallel to the track, which is W sin , or mg sin . This must be equal to ma, where m is the skier's mass, and a is the skier's acceleration down the track. So we have mg sin = ma. Note that the m terms cancel, so the result does not depend on the mass, and is the same for all skiers. In the question

  

  stem, we are told that = 45? Substituting into the equation a = g sin , we get that a = 9.8, or 4.9 . At this point we must approximate, since we don't know what . We know that it is going to be less than two but greater than one, which tells us that a is between 4.9 and 9.8 m/s2. The only answer choice that is applicable here is answer choice A, 6.9 m/s2.

• Question 329:

  Aski jump is an inclined track from which a ski jumper takes off through the air. After traveling down the track, the skier takes off from a ramp at the bottom of the track. The skier lands farther down on the slope.

  Figure 1 shows a ski jump, in which the ramp at the lower end of the track makes an angle of 30° to the horizontal. The track is inclined at an angle of to the horizontal and the slope is inclined at an angle of 45° to the horizontal. A ski jumper is stationary at the top of the track. Once the skier pushes off, she accelerates down the track, and then takes off from the ramp. The vertical height difference between the top of the track and its lowest point is 50 m, and the vertical height difference between the top of the ramp and its lowest point is 10 m.

  

  Figure 1

  The distance traveled by the skier between leaving the ski jump ramp and making contact with the slope is called the jump distance. In some cases, in order to increase the jump distance a skier will jump slightly upon leaving the ramp, thereby increasing the vertical velocity. Unless otherwise stated, assume that friction between the skis and the slope is negligible, and ignore the effects of air resistance.

  If a skier uses skis of greater surface area, which of the following would occur?

  A. The normal force of the slope on the skier would increase.

  B. The normal force of the slope on the skier would decrease.

  C. The pressure exerted on the slope by the skis would increase.

  D. The pressure exerted on the slope by the skis would decrease.

  Correct Answer: D

  The only condition that changes in this question is the surface area of the skis. The normal force of the slope on the skier depends only on the mass of the skier, the acceleration due to gravity, and the angle of the slope. Therefore, changing the surface area of the skis would not affect the normal force, and choices A and B are incorrect. Therefore, the pressure exerted on the slope by the skis must depend on the surface area of the skis. The exact relationship is P = F/A, where P is the pressure on the slope due to the skis, F is the force exerted by the skis on the slope, and A is the surface area over which the force acts, which in this case is the surface area of the skis. The force exerted by the skis is just the component of the weight of the skier normal to the slope, or the normal force, which is constant. Therefore, the pressure is inversely proportional to the surface area of the skis. So the pressure decreases as the surface area increases, choice

  D.

• Question 330:

  Aski jump is an inclined track from which a ski jumper takes off through the air. After traveling down the track, the skier takes off from a ramp at the bottom of the track. The skier lands farther down on the slope.

  Figure 1 shows a ski jump, in which the ramp at the lower end of the track makes an angle of 30?to the horizontal. The track is inclined at an angle of to the horizontal and the slope is inclined at an angle of 45?to the horizontal. A ski jumper is stationary at the top of the track. Once the skier pushes off, she accelerates down the track, and then takes off from the ramp. The vertical height difference between the top of the track and its lowest point is 50 m, and the vertical height difference between the top of the ramp and its lowest point is 10 m.

  Figure 1

  

  The distance traveled by the skier between leaving the ski jump ramp and making contact with the slope is called the jump distance. In some cases, in order to increase the jump distance a skier will jump slightly upon leaving the ramp, thereby increasing the vertical velocity. Unless otherwise stated, assume that friction between the skis and the slope is negligible, and ignore the effects of air resistance.

  Which of the following would increase the jump distance?

  I) Increasing the vertical height h of the jump track II) Increasing the angle of incline of the jump track III) Carrying extra weight to increase the total mass of the ski jumper

  A. I only

  B. I and II only

  C. II and III only

  D. I and III only

  Correct Answer: A

  Statement I says that increasing the vertical height h of the jump track would increase the jump distance. This is true. If we increase the vertical height h of the jump track, we give the ski jumper a greater initial potential energy, and therefore increase the overall change in potential energy. This means that the ski jumper's kinetic energy at the point that she takes off is greater, and thus her take-off speed is greater. If her take-off speed increases, then the jump distance must also increase. Since Statement I is true, we can eliminate choice C. Statement II says that increasing the angle of incline of the jump increases the jump distance. This is untrue. By increasing the angle of incline, we do not increase the maximum potential energy of the ski jumper, and therefore the kinetic energy at the end of the ramp remains unaltered. Potential energy only depends on vertical height h, and not on how steep or how shallow the incline is. Therefore, the take-off speed is not increased, and the jump distance is not increased. Since Statement II is false we can eliminate choice B. Statement III states that increasing the total mass of the ski jumper increases the jump distance. As we saw in the answer to the previous question, the mass term cancels, which implies that all objects are accelerated at the same rate, irrespective of their mass. In other words, a ski jumper with a mass of 60 kilograms will have the same take-off speed as a ski jumper with a mass of 100 kilograms. Therefore, Statement III is false, and choice A is the correct answer.