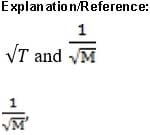Medical Tests Medical Tests Certifications MCAT-TEST Questions & Answers

• Question 361:

  The periodic beating of the heart is controlled by electrical impulses that originate within the cardiac muscle itself. These pulses travel to the sinoatrial node and from there to the atria and the ventricles, causing the cardiac muscles to contract. If a current of a few hundred milliamperes passes through the heart, it will interfere with this natural system, and may cause the heart to beat erratically. This condition is known as ventricular fibrillation, and is life-threatening. If, however, a larger current of about 5 to 6 amps is passed through the heart, a sustained ventricular contraction will occur. The cardiac muscle cannot relax, and the heart stops beating. If at this point the muscle is allowed to relax, a regular heartbeat will usually resume.

  The large current required to stop the heart is supplied by a device known as a defibrillator. A schematic diagram of a defibrillator is shown below. This device is essentially a "heavy-duty" capacitor capable of storing large amounts of energy. To charge the capacitor quickly (in 1 to 3 seconds), a large DC voltage must be applied to the plates of the capacitor. This is achieved using a step-up transformer, which creates an output voltage that is much larger than the input voltage. The transformer used in this defibrillator has a step-up ratio of 1:50.

  

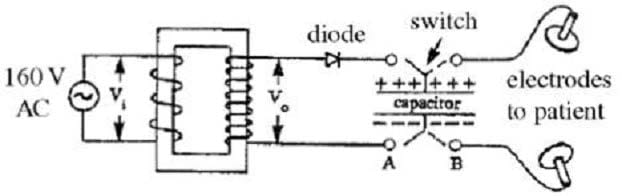
  The AC voltage that is obtained from the transformer must then be converted to DC voltage in order to charge the capacitor. This is accomplished using a diode, which allows current flow in one direction only. Once the capacitor is fully charged, the charge remains stored until the switch is moved to position B and the plates are placed on the patient's chest. To cut down the resistance between the patient's body and the defibrillator, the electrodes are covered with a wetting gel before use. Care must be taken to insure that the patient is not in electrical contact with the ground while the defibrillator is in use.

  Why is it important to insure that the patient is not in electrical contact with the ground while the defibrillator is in use?

  A. Contact with the ground will decrease the resistance across the patient's body.

  B. The doctor administering the treatment will be in greater danger of receiving an electric shock if the patient is in electrical contact with the ground.

  C. Contact with the ground will cause a smaller current to pass through the patient's heart.

  D. The patient receiving the treatment will be in greater danger of receiving burns due to the high current density if he is in electrical contact with the ground.

  Correct Answer: C

  When there is no ground connection, all the current is forced through the patient's heart, despite the relatively large resistance of the patient's body. However, if the patient is in contact with the ground, this provides a path of far less resistance than the patient's body, resulting in most of the current flowing through the ground, rather than through the patient. This will render the defibrillator ineffective. Choice A is incorrect because the resistance across the patient's body cannot change. Choice B is incorrect. If the defibrillator is not in contact with the patient when the doctor receives a shock, then the shock hazard has nothing to do with the patient being grounded or not. If, however, the electrodes are in contact with the patient when the doctor receives a shock, the ground will take most of the current, and thereby reduce the shock that the doctor experiences. So the doctor administering the treatment will be in less danger of receiving a shock when the patient is in contact with the ground. Choice D is incorrect since the burns received by the patient are due to the application of large currents over a small area of skin, and have nothing to do with the presence of a ground. Therefore, in order to reduce the burns that the patient receives, the area of the electrodes is increased to distribute the current and reduce the current density. The correct answer is choice C, contact with the ground will cause a smaller current to pass through the patient's heart.

• Question 362:

  The periodic beating of the heart is controlled by electrical impulses that originate within the cardiac muscle itself. These pulses travel to the sinoatrial node and from there to the atria and the ventricles, causing the cardiac muscles to contract. If a current of a few hundred milliamperes passes through the heart, it will interfere with this natural system, and may cause the heart to beat erratically. This condition is known as ventricular fibrillation, and is life-threatening. If, however, a larger current of about 5 to 6 amps is passed through the heart, a sustained ventricular contraction will occur. The cardiac muscle cannot relax, and the heart stops beating. If at this point the muscle is allowed to relax, a regular heartbeat will usually resume.

  The large current required to stop the heart is supplied by a device known as a defibrillator. A schematic diagram of a defibrillator is shown below. This device is essentially a "heavy-duty" capacitor capable of storing large amounts of energy. To charge the capacitor quickly (in 1 to 3 seconds), a large DC voltage must be applied to the plates of the capacitor. This is achieved using a step-up transformer, which creates an output voltage that is much larger than the input voltage. The transformer used in this defibrillator has a step-up ratio of 1:50.

  

  The AC voltage that is obtained from the transformer must then be converted to DC voltage in order to charge the capacitor. This is accomplished using a diode, which allows current flow in one direction only. Once the capacitor is fully charged, the charge remains stored until the switch is moved to position B and the plates are placed on the patient's chest. To cut down the resistance between the patient's body and the defibrillator, the electrodes are covered with a wetting gel before use. Care must be taken to insure that the patient is not in electrical contact with the ground while the defibrillator is in use.

  If the defibrillator has a capacitance of 10 F, how much charge will build up on the two plates?

  A. 0.08 coulombs

  B. 0.8 coulombs

  Correct Answer: A

  The correct answer choice here is A, 0.08 coulombs. To do this question, you must remember the equation Q = CV, where Q is the charge stored, C is the capacitance, and V is the voltage across the plates. We are given that the capacitance is 10 micro farads, but we do not have a value for the voltage V, since the input voltage to the transformer is stepped-up 50 times. From the diagram we can see that the input voltage is 160 volts. So the output voltage is 160 times 50, or 8,000 volts. Substituting the voltage and the capacitance into our equation, gives a value for the charge of 8,000 times 10x10-6, or 0.08 coulombs, choice A.

• Question 363:

  The periodic beating of the heart is controlled by electrical impulses that originate within the cardiac muscle itself. These pulses travel to the sinoatrial node and from there to the atria and the ventricles, causing the cardiac muscles to contract. If a current of a few hundred milliamperes passes through the heart, it will interfere with this natural system, and may cause the heart to beat erratically. This condition is known as ventricular fibrillation, and is life-threatening. If, however, a larger current of about 5 to 6 amps is passed through the heart, a sustained ventricular contraction will occur. The cardiac muscle cannot relax, and the heart stops beating. If at this point the muscle is allowed to relax, a regular heartbeat will usually resume.

  The large current required to stop the heart is supplied by a device known as a defibrillator. A schematic diagram of a defibrillator is shown below. This device is essentially a "heavy-duty" capacitor capable of storing large amounts of energy. To charge the capacitor quickly (in 1 to 3 seconds), a large DC voltage must be applied to the plates of the capacitor. This is achieved using a step-up transformer, which creates an output voltage that is much larger than the input voltage. The transformer used in this defibrillator has a step-up ratio of 1:50.

  

  The AC voltage that is obtained from the transformer must then be converted to DC voltage in order to charge the capacitor. This is accomplished using a diode, which allows current flow in one direction only. Once the capacitor is fully charged, the charge remains stored until the switch is moved to position B and the plates are placed on the patient's chest. To cut down the resistance between the patient's body and the defibrillator, the electrodes are covered with a wetting gel before use. Care must be taken to insure that the patient is not in electrical contact with the ground while the defibrillator is in use.

  The resistance between the two electrodes when placed apart on the patient's chest is 1,000 when wetting gel is used. What is the initial current through the patient's heart, assuming that all the current takes this path?

  A. 0.16 A

  B. 4 A

  C. 6.25 A

  D. 8 A

  Correct Answer: D

  This question asks you to calculate the initial current through the patient, and this can be done by using Ohm's law which states that the current is equal to the voltage divided by the resistance. We know that the resistance across the two electrodes is 1000 ohms when a wetting gel is applied, but as in the previous question we do not have a value for the initial voltage. This be calculated as well. We know that the transformer increases the input voltage by a factor of 50, and since the input voltage is 160 volts, the output voltage will be 8000 volts. This voltage charges the capacitor only, so the voltage across the capacitor when fully charged will be 8000 volts. By substituting the values for the resistance and the voltage into Ohm's law, we find that the initial current flowing through the patient is 8000 divided by 1000, or 8 amps which is choice D.

• Question 364:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision. The average kinetic energy (E) of a gas particle is given by:

  

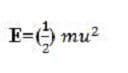
  Equation 1

  where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles:

  

  where N is the number of gas particles; this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:

  

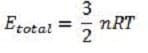
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

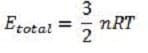
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

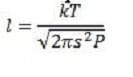
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

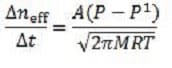
  Equation 5

  Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1.

  Which of the following will have the smallest root mean square speed at 298K?

  

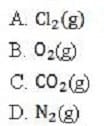
  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: A

  

  Equation 3 states that the root mean square speed, u, is equal to (3RT/M)? Therefore, u is proportional to . Since the temperature is held constant, we must look at the molar mass. If u is proportional to the molecule with the largest molar mass will have the smallest root mean square speed. Chlorine, choice A, has the largest molar mass (71 g/mol) and is the correct response. Oxygen, carbon dioxide, and nitrogen have molar masses of 32 g/mol, 44 g/ mol, and 28 g/mol, respectively. When compared with chlorine, we can see that all of these molecules will have a larger root mean square speed.

• Question 365:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision.

  The average kinetic energy (E) of a gas particle is given by:

  Equation 1

  where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles:

  

  where N is the number of gas particles; this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:

  

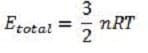
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

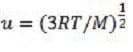
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

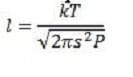
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

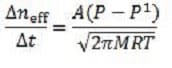
  Equation 5

  Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1.

  What is the relative rate of effusion for a mixture of two noble gases, GA and GB, which escape through the same pinhole?

  

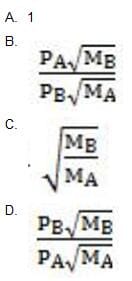
  A. Option A

  B. Option B

  C. Option C

  D. Option D

  Correct Answer: C

  If the ratio of the rates of effusion for the two gases is taken, and all factors that are the same for the two gases are canceled out, then one ends up simply with the inverse of the square root of the masses, as in choice C. Since the gases A and B constitute a mixture, they are in the same container, at the same pressure and effusing through the same pinhole. Therefore, the pinhole area for A equals the pinhole area of B, and the answer given in choice B can be condensed to the answer given in choice C. Similarly, the pressure of the gas in the container is the same whether you are considering the gas A component or the gas B component, since they are in a mixture characterized by one pressure. Thus, the answer given in choice D also reduces to that in choice C. Choice A, which states that the ratio is 1, would only be correct if the two gases being considered had the same molecular weight. Although it is possible for this to be true, we have no indication of whether or not it is. Since the question states that they are two noble gases, it is safer to assume that the two gases have different molecular weights.

• Question 366:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision. The average kinetic energy (E) of a gas particle is given by:

  

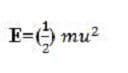
  Equation 1

  where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles:

  

  where N is the number of gas particles; this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:

  

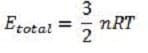
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

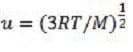
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

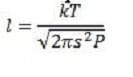
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

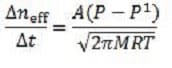
  Equation 5

  Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1.

  The average kinetic energy of an ideal gas can be directly related to the:

  A. rms speed.

  B. temperature.

  C. Boltzmann constant.

  D. universal gas constant.

  Correct Answer: B

  Equation 2 gives the formula for the average kinetic energy of an ideal gas. To answer this question, all you have to do is figure out which factor varies directly with the average kinetic energy. The rms speed, u, has been canceled out of this equation, so choice A is wrong. The Boltzmann constant had universal gas constant, choices C and D, are the same for every value of the average kinetic energy, so they are also wrong. That leaves only temperature, choice B, the correct answer. All that is needed to obtain the correct answer is Equation 2 and an understanding of the various variables in the equation. However, choice B may have been your instinctive choice since a study of gases always mentions that the temperature of a gas is a measure of the average kinetic energy of that gas. Either way, the correct answer is B.

• Question 367:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision. The average kinetic energy (E) of a gas particle is given by:

  

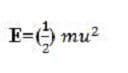
  Equation 1

  where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles: where N is the number of gas particles;

  

  this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:

  

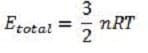
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

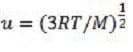
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

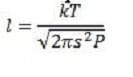
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

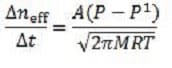
  Equation 5

  Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1.

  The mean free path of a gas will be longer if the :

  A. pressure of the gas is increased.

  B. number of gas particles per unit volume is increased.

  C. distance between collisions is decreased.

  D. pressure of the gas is decreased.

  Correct Answer: D

  The mean free path of a particle is the average distance the particle can travel before it collides with another gas particle or the wall of the container. The longer the distance that a gas particle travels between collisions, the further apart the individual gas molecules must be. That means that the volume of the gas must increase to increase the distance between collisions. One way to increase the volume is to decrease the pressure of the gas, so D is correct. Choice A is incorrect because an increase in pressure leads to a decrease in the volume and thus a decrease in mean free path as well. Thus the gas particles are closer together and are more likely to collide, decreasing the average distance they travel between collisions. Choice B is incorrect because if the number of particles is increased while the volume remains constant, the likelihood of a collision will also increase. The pressure also increases as the number of particles per unit volume increases. Choice C is incorrect because the mean free path is analogous to the distance between collisions and if this is decreased then the mean free path decreases s well. Basically, choices A, B and C will all decrease the mean free path of a gas, making them all incorrect.

• Question 368:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

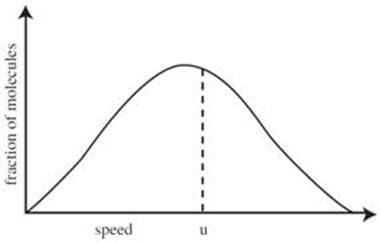
  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision. The average kinetic energy (E) of a gas particle is given by:

  

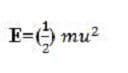
  Equation 1

  where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles:

  

  where N is the number of gas particles; this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:

  

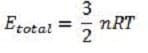
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

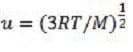
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

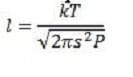
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

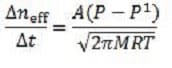
  Equation 5

  Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1.

  Which of the following gives values for both standard temperature and pressure?

  A. 273 K and 760 Torr

  B. 273 K and 1 atm

  C. 0°C and 760 mm Hg

  D. All of the above

  Correct Answer: D

  Standard temperature is usually expressed in either Celsius or Kelvin; for pressure, there are 3 different commonly used units. These are Torr, atmospheres, and millimeters of mercury. Conversion to other commonly used units is possible given standard temperature and pressure in one set of units. Conversion factors were not given in this problem because it is general knowledge that 1 atmosphere of pressure is equal to 760 Torr and 760 millimeters of mercury. To convert from Celsius to Kelvin, simply add 273. If you recall that standard temperature is 0 degrees Celsius, then it is a simple matter to convert to Kelvin to get choice D.

• Question 369:

  The equation of state of an ideal gas is given by the ideal gas law:

  PV = nRT

  where P is the pressure, V is the volume, n is the number of moles of gas, R is the ideal gas constant, and T is the temperature of the gas. The gas particles in a container are constantly moving at various speeds. These speeds are

  characterized by the Maxwell shown in the figure below.

  

  If two particles collide, their velocities change. However, if the gas is in thermal equilibrium, the velocity distribution of the gas as a whole will remain unchanged by the collision. The average kinetic energy (E) of a gas particle is given by:

  

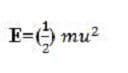
  Equation 1 where m is the mass of one particle and u is the root mean square speed (rms speed) of the gas particles

  

  where N is the number of gas particles; this is different from the average speed). For an ideal gas, the kinetic energy of all the particles is:Z

  

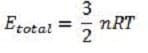
  Equation 2

  where n is the number of moles of gas. Combining these equations gives:

  

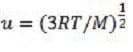
  Equation 3

  where M is the molar mass of the gas particles.

  The average distance a particle travels between collisions is known as the mean free path l. Intuitively, the mean free path (mfp) could be expected to be larger for gases at low pressure, since there is a lot of space between particles.

  Similarly, the mfp should be larger when the gas particles are small. The following expression for the mfp shows this to be correct.

  

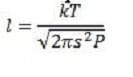
  Equation 4 In this equation, s is the atomic diameter (typically on the order of 10?), k is the Boltzmann constant, and P is the pressure. In addition to colliding with one another, gas particles also collide with the walls of their container. If the container wall has a pinhole that is small compared to the mfp of the gas, and a pressure differential exists across the wall, the particles will effuse (or escape) through this pinhole without disturbing the Maxwellian distribution of the particles. The rate of effusion can be described by:

  

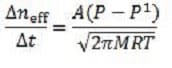
  Equation 5 Where neff is the number of moles of effusing particles, A is the area of the pinhole, p and p1 are the pressures on the inside and outside of the container wall respectively, and p>p1. If a pinhole were made in a container containing a mixture of equal amounts of H2, O2, N2 and CO2, which gas would have the fastest effusion rate?

  A. H2

  B. O2

  C. N2

  D. Co2

  Correct Answer: A

  According to Equation 5, the rate of effusion depends on the area of the pinhole, the pressures inside and outside the container, the molecular weight of the particles, the gas constant R, and the temperature. Since all 4 gases are in one container, subject to the same conditions, the only one of these factors that is different for the 4 gases is molecular weight. Since the rate of effusion is inversely proportional to the square root of the molecular weight, the rate of effusion increases as the molecular weight decreases. Thus, the lightest particle will effuse through the pinhole fastest. Molecular hydrogen is the lightest of the four species, with a molecular weight of 2 grams per mole, so it will effuse the fastest and choice A is the correct answer.

• Question 370:

  Which of the following neurotransmitters could be imbalanced if someone woke up and realized they could not move any muscle?

  A. Catecholamine

  B. Acetylcholine

  C. Frataxin

  D. Cortisol

  Correct Answer: B

  B is correct. Acetylcholine is a neurotransmitter. It is released by the neurons. It then synapses at the muscular junctions and provokes the contraction of the skeletal motor cells. It is critical for motor movement. Its absence or blockage (for example, via antagonist drugs) would cause paralysis. A. This is incorrect. Catecholamines are neurotransmitters (such as adrenaline, dopamine, and noradrenaline) that have been found to have a role in the flight-or-fight response to stressful stimuli. Specifically, they are involved in the flight response and responsible for the activation of the sympathetic nervous system. They are not critical for skeletal muscle control. C. This is incorrect. Frataxin is one protein which may cause paralysis. It is not a neurotransmitter. D. This is incorrect. Cortisol is a hormone that has been found to have a role in the flight-or-fight response to stressful stimuli. Specifically, it is involved in the flight response and responsible for the activation of the sympathetic nervous system. It is not critical for skeletal muscle control.